
|
MUSIC CLASSIFICATOIN BY GENRE USING NEURAL NETWORKS An example of a multivariate data type classification problem using Neuroph framework by Marina Jeremić, Faculty of Organizational Sciences, University of Belgrade an experiment for Intelligent Systems course Introduction
Neural networks have found profound success in the area of pattern recognition. By repeatedly showing a neural network inputs classified into groups, the network can be trained to discern the criteria used to classify, and it can do so in a generalized manner allowing successful classification of new inputs not used during training. With the explosion of digital music in recent years due to Napster and the Internet, the application of pattern recognition technology to digital audio has become increasingly interesting.
Digital music is becoming more and more popular in people’s life. It is quite common for a person to own thousands of digital music pieces these days, and users may build their own music library through music management systems or software such as the Music Match Jukebox. However for professional music databases, labors are often hired to manually classify and index music assets according to predefined criteria; most users do not have the time or patience to browse through their personal music collections and manually index the music pieces one by one. On the other hand, if music assets are not properly classified, it may become a big headache when the user wants to search for a certain music piece among the thousands of pieces in a music collection. Manual classification methods cannot meet the development of digital music. Music classification is a pattern recognition problem which includes extraction features and establishing classifier. Many researchers have done a lot of works in this field and put forward some methods such as the rule-based audio classification method, the pattern match method, Hidden Markov Models (HMM), but they have own shortcomings, for example, rule-based audio classification can only be applied to identify the audio genres with simple characteristics, such as mute, so it is very difficult to meet the requirements of complex and multi-feature music. Pattern matching method needs to establish a standard mode for each audio type, so the calculation amount is large and classification accuracy is low. HMM method has poor
classification decision ability and needs priori statistical knowledge. Artificial neural network have found profound success in the area of pattern recognition, it can be trained to discern the criteria used to classify, and can do so in a generalized manner by repeatedly showing a neural network inputs classified into groups. Neural network provides a new solution for music classification, so a new music classification method is proposed based on BP neural network in this experiment. Introduction to the problem
We will use Neuroph framework for training the neural network that
uses music songs data set.
Data set contains features from symbolic songs (MP3, in this case) and uses them to classify the recordings by genre. Each example is classified as classic, rock, jazz or folk song. Further, there will be different data sets depending of features which will be taken.The attributes are duration of song, tempo, root mean square (RMS) amplitude, sampling frequency, sampling rate, dynamic range, tonality and number of digital errors. Main goal of this experiment is to train neural network to classify this 4 type of genre and to discover which observed features has impact on classification. Attribute Information:
Procedure of training a neural network
In order to train a neural network, there are six steps to be made:
In this experiment we will demonstrate the use of some standard and advanced training techniques. Step 1. Data Normalization
In order to train neural network this data set have to be normalized.
Normalization implies that all values from the data set should take
values in the range from 0 to 1. For that purpose it would be used the following formula: 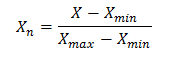
Where: X – value that should be normalizedXn – normalized value Xmin – minimum value of X Xmax – maximum value of X Last 4 digits of data set represent genre. 1 0 0 0 represent rock genre, 0 1 0 0 classic genre, 0 0 1 0 jazz and 0 0 0 1 folk genre. Step 2. Creating a new Neuroph project
The steps below outline how to create a Neuroph project using many of the default settings to make it easy to get started.
Step 3. Creating a Training Set
To create training set, in project menu we choose Training sets, then click New
File icon, choose category Neuroph ant type Training set, then click Next to continue with training set wizard. Then we enter name of
training set and number of inputs and outputs. In this case it will be 8
inputs,then 4 inputs and finally 5 inputs and 4 outputs in all cases and we will set type of training to be supervised
as the most common way of neural network training.
As supervised training proceeds, the neural network is taken through a number of iterations, until the output of the neural network matches the anticipated output, with a reasonably small rate of the error. 
After clicking 'Next' we need to insert data into training set table. All data could be inserted manually, but we have a large number of data instances and it would be a lot more easier to load all data directly from some file. We click on Choose File and select file in which we saved our normalized data set. Values in that file are separated by tab. Then, we click 'Load' and all data will be loaded into table. We can see that this table has 12 columns, first 8 of them represents inputs, and last 4 of them represents outputs from our data set. 
After clicking 'Finish' new training set will appear in our project. To achieve the main goal and decide which is the best solution for this problem it will be created several neural networks, with different sets of parameters, and they will be based on different training sets. First training set will contain all attributes above, second training set will contain just tempo, RMS, dynamic range and number of digital errors, and to third will be added tonality. Standard training techniques
Standard approaches to validation of neural networks are mostly based on empirical evaluation through simulation and/or experimental testing. There are several methods for supervised training of neural networks. The backpropagation algorithm is the most commonly used training method for artificial neural networks. Backpropagation is a supervised learning method. It requires a dataset of the desired output for many inputs, making up the training set. It is most useful for feed-forward networks (networks that have no feedback, or simply, that have no connections that loop). The term is an abbreviation for "backward propagation of errors". Backpropagation requires that the activation function used by the artificial neurons (or "nodes") be differentiable. As the algorithm's name implies, the errors propagate backwards from the output nodes to the inner nodes. Technically speaking, backpropagation calculates the gradient of the error of the network regarding the network's modifiable weights. This gradient is almost always used in a simple stochastic gradient descent algorithm to find weights that minimize the error. Often the term "backpropagation" is used in a more general sense, to refer to the entire procedure encompassing both the calculation of the gradient and its use in stochastic gradient descent. Backpropagation usually allows quick convergence on satisfactory local minima for error in the kind of networks to which it is suited. Backpropagation networks are necessarily multilayer perceptrons (usually with one input, one hidden, and one output layer). In order for the hidden layer to serve any useful function, multilayer networks must have non-linear activation functions for the multiple layers: a multilayer network using only linear activation functions is equivalent to some single layer, linear network. Non-linear activation functions that are commonly used include the logistic function, the softmax function, and the gaussian function. The backpropagation algorithm for calculating a gradient has been rediscovered a number of times, and is a special case of a more general technique called automatic differentiation in the reverse accumulation mode. It is also closely related to the Gauss–Newton algorithm, and is also part of continuing research in neural backpropagation. Training attempt 1 - all observed features
Step 4.1 Creating a neural network
We create a new neural network by clicking right click on project and
then New > Neural Network. Then we define neural network name and
type. We will choose Multy Layer Perceptron type. A multilayer perceptron(MLP) is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate output. An MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a neuron (or processing element) with a nonlinear activation function. MLP utilizes a supervised learning technique called backpropagation for training the network. MLP is a modification of the standard linear perceptron, which can distinguish data that is not linearly separable. 
In the next window of wizard we will set multy layer perceptron's parameters. The number of input and output neurons are the same as in the training set. And now we have to choose number of hidden layers, and number of neurons in each layer. Main question is -How to choose the number of hidden layers and nodes in a neural network? The Input Layer Simple - this layer configuration is completely and uniquely determined once we know the shape of our training data. Specifically, there's only one input layer, and the number of neurons comprising that layer is equal to the number of dimensions (columns) in our data. Some NN configurations add one additional node for a bias term. The Output Layer NN's have only one of them. It's size (number of neurons) is completely determined by the chosen model configuration. It is set to 4, which is equal to the number of elements in the target vector (the number of categories, genres). The Hidden Layers So those few rules set the number of layers and size (neurons/layer) for both the input and output layers. That leave the hidden layers. How many hidden layers? Well if your data is linearly separable (which you often know by the time you begin coding a NN) then you don't need any hidden layers at all. Of course, you don't need an NN to resolve your data either, but it will still do the job. Beyond that, as you probably know, there's a mountain of commentary on the question of hidden layer configuration in NNs. One issue within this subject on which there is a consensus is the performance difference from adding additional hidden layers: the situations in which performance improves with a second (or third, etc.) hidden layer are very small. One hidden layer is sufficient for the large majority of problems. So what about size of the hidden layer(s)-how many neurons? There are some empirically-derived rules-of-thumb, of these, the most commonly relied on is 'the optimal size of the hidden layer is usually between the size of the input and size of the output layers'. Jeff Heaton, author of Introduction to Neural Networks in Java offers a few more. In sum, for most problems, one could probably get decent performance (even without a second optimization step) by setting the hidden layer configuration using just two rules: (i) number of hidden layers equals one; and (ii) the number of neurons in that layer is the mean of the neurons in the input and output layers. Optimization of the Network Configuration Pruning describes a set of techniques to trim network size (by nodes not layers) to improve computational performance and sometimes resolution performance. The gist of these techniques is removing nodes from the network during training by identifying those nodes which, if removed from the network, would not noticeably affect network performance (i.e., resolution of the data). (Even without using a formal pruning technique, you can get a rough idea of which nodes are not important by looking at your weight matrix after training; look weights very close to zero-it's the nodes on either end of those weights that are often removed during pruning.) Obviously, if you use a pruning algorithm during training then begin with a network configuration that is more likely to have excess (i.e., 'prunable') nodes-in other words, when deciding on a network architecture, err on the side of more neurons, if you add a pruning step. Put another way, by applying a pruning algorithm to your network during training, you can approach optimal network configuration; whether you can do that in a single "up-front" (such as a genetic-algorithm-based algorithm) i don't know, though i do know that for now, this two-setp optimization is more common. We’ve decided to have 1 layer and 4 neurons in this first training attempt. Than we check 'Use Bias Neurons' option and choose 'Sigmond' for transfer function (because our data set is normalized). For learning rule we choose 'Backpropagation with Momentum'. The momentum is added to speed up the process of learning and to improve the efficiency of the algorithm. Bias neuron is very important, and the error-back propagation neural network without Bias neuron for hidden layer does not learn. The Bias weights control shapes, orientation and steepness of all types of Sigmoidal functions through data mapping space. A bias input always has the value of 1. Without a bias, if all inputs are 0, the only output ever possible will be a zero. 
Next, we click 'Finish' and the first neural network is created. In the picture below we can see the graph view of this neural network.  Figure shows the input, the output and hidden neurons and how they are connected with each other. Except for two neurons with activation level 1 (bias activation), all other neurons have an activation level 0. These two neurons represent bias neurons, as we explained above. Step 5.1 Train the neural network
After we have created training set and neural network we can train neural network. First, we select training set(all features), click 'Train', and then we have to set learning parameters for training. Learning rate is a control parameter of training algorithms, which controls the step size when weights are iteratively adjusted. To help avoid settling into a local minimum, a momentum rate allows the network to potentially skip through local minima. A momentum rate set at the maximum of 1.0 may result in training which is highly unstable and thus may not achieve even a local minima, or the network may take an inordinate amount of training time. If set at a low of 0.0, momentum is not considered and the network is more likely to settle into a local minimum. When the Total Net Error value drops below the max error, the training is complete. If the error is smaller we get a better approximation. In this first case a maximum error will be 0.04, learning rate 0.2 and momentum 0.7. 
Then we click on the Train button and the training process starts. 
After 2570 iterations Total Net Error drop down to a specified level of 0.04 which means that training process was successful and that now we can test this neural network. Step 6.1 Test the neural network
We test neural network by choosing the test data set and clicking on the Test button, and then we can see testing results. In the results we can see that the Total Mean Square Error is 0.0259347225703999. That certainly is not a very good result, because our goal is to get the total error to be as small as possible. 
Looking at the individual errors we can observe that most of them are at the low level, below 0.1, but there are also some cases where those errors are considerably larger. So we can conclude that this type of neural network architecture is not the best choice and we should try some other so we could managed to reach the best solution for our problem. Training attempt 2 - all observed features
Step 5.2 Train the neural network
In our second attempt we will only change some learning parameters and then will see what happens. We will decrease the value of a maximum error to 0.03, learning rate will be 0.5 and momentum 0.4. After only 2358 iterations it was reached the max error. 
Step 6.2 Test the neural network
Now we want to see testing results. 
In this attempt the total mean square error is lower then it was in previous case. We should try some other architecture in order to get better results, because many variations with learning parameters we tried on this architecture were not successful, in terms of reaching max error. Training attempt 3 - all observed features
Step 4.3 Creating a neural network
In this attempt we will try to get some better results by increasing the size of hidden neurons. It is known that number of hidden neurons is crucial for network training success, and now we will try with 6 hidden neurons. First we have to create a new neural network. All the parameters are the same as they were in the first training attempt, we will just change the number of hidden neurons. 
 Step 5.3 Train the neural network
In our first training of this second neural network architecture we will try with the same learning parameters as in the first of all training attemps, but max error will be 0.01.  
Training process starts, and after 956 iterations it was reached the max error that was given. Step 6.3 Test the neural network
Now, we will test this neural network and see testing results for this neural network architecture. 
In this case the total mean square error is lower than it was in the last training attempt, but generally the overall result is still not so good. Also, we can see that there are lot of the individual errors that are very high so we will have to try some other learning parameters that will give as a better testing results. Training attempt 4 - all observed features
Step 5.4 Train the neural network
Neural network that we've created in last attempt can now be trained. In this attempt we will set learning parameters as in the picture that is above.  It took 7409 iterations for network to train.  Step 6.4 Test the neural network
After testing the neural network, we see that the total mean square error is 0.01914222314021746 which is not the best of all than it was in the previous attempts, but almost all songs are classified correctly. 
Training attempt 5 - tempo, root mean square (RMS) amplitude, dynamic range and number of digital errors
Step 3.5 Creating a training set
Now, we will use different data set in same proportions of data amount. Features of music songs which we will take, would be just only those for which we believe they have a decisive influence on the classification, actually those are tempo, root mean square (RMS) amplitude, dynamic range and number of digital errors, but we are not sure if tonality impact on classification, and for these reasons later there will be one more variation of data set. There is only 4 inputs and 4 outputs  Step 4.5 Creating a neural network
Next step is creation of new network which will have 4 input neurons, 20 hidden and 4 output neurons, as you see in fallowing picture  Step 5.5 Train the neural network
In this attempt we will use upper network architecture. We will try to get as better results as it can by adjustment some learning parameters. For learning rate now we will set 0.5, and momentum will be 0.7, the max error will be 0.04. 
Step 6.5 Test the neural network
After testing, we got that in this attempt the total error is 0.04220659072705381. 
We tried many different architecture, but always when number of hidden neurons were smaller than 18, it was imposible to achieve a given max error. Training attempt 6 - tempo, root mean square (RMS) amplitude, dynamic range and number of digital errors
Step 5.6 Train the neural network
This neural network architecture is the same as previous, has 20 hidden neurons, which is even bigger than the sum of inputs and outputs. We think that it should be enough for network to, for the first time, reach the maximum error of 0.01. Learning rate will be 0.5 and momentum 0.8. In this case we will limit the max error to 0.01. Then we will try to train network, and see what happens. 
Network was successfully trained, and finally, after 280 iterations, it was reached a desired error - under 0.01! In the total network error graph we can see that the error decreases continuously throughout the whole training cycle. 
Step 6.6 Test the neural network
We are very interested to see the testing results for this type of neural network architecture. In the training process, the total mean square error was below 0.02, and that could also indicate a better testing results! After we have finish testing we can see that the total mean square error in this case is 0.011984081858225411, and that certainly is a better than the errors in previous attempts. In this testing process were involved 10 songs but 5 of this are classified correctly and other half is classified with minor errors. 
Training attempt 7 - tempo, root mean square (RMS) amplitude, tonality, dynamic range and number of digital errors
Step 4.7 Creating a neural network
For this type of problem, where we have 5 inputs, we need different architecture, with 5 input neurons, in this case we tried many of them, and finally took structure with 10 hidden neurons 
Step 5.7 Train the neural network
With this training attempt we will try to reduce the total error by changing some of the learning parameters. Empirically we have decide that limitation for the max error will be 0.01, we will set the learning rate to 0.2 and momentum will be 0.7. 
As we can see in the image below, network was successfully trained, and finally after 19450 iterations the total error was reduced to the level below 0.01. 
Step 6.7 Test the neural network
After testing neural network, we see that in this attempt the total mean square error is about 0.000409, which is much better than the error that was in the previous attempt, were tonality wasn't involved in dataset. 
In this training attempt we saw that even after many iterations in training process, testing results are great 10 of 10 songs are right classified in genres that belong to. For the first time, we will random choose 5 observations which will be subjected to individual testing. Those observations and their testing results are in the following table: 
As we can see in the table, the network guessed right in all five cases, so we can conclude that this type of neural network architecture is very good. Advanced training techniques
Neural networks represent a class of systems that do not fit into the current paradigms of software development and certification. Instead of being programmed, a learning algorithm “teaches” a neural network using a set of data. Often, because of the non-deterministic result of the adaptation, the neural network is considered a “black box” and its response may not be predictable. Testing the neural network with similar data as that used in the training set is one of the few methods used to verify that the network has adequately learned the input domain. One method that is used by neural network developers is to separate a set of available data into three sets: training, validation, and testing sets. The training set is used as the primary set of data that is applied to the neural network for learning and adaptation. The validation set is used to further refine the neural network construction. The testing set is then used to determine the performance of the neural network by computation of an error metric. The validation set contains a smaller percentage of instances from the initial data set, and is used to determine whether the selected network architecture is good enough. If validation was successful, only then we can do the training. The training set is applied to the neural network for learning and adaptation. The testing set is then used to determine the performance of the neural network by computation of an error metric. This validating-training-testing approach is the first, and often the only, option system developers consider for the assessment of a neural network. The assessment is accomplished by the repeated application of neural network training data, followed by an application of neural network testing data to determine whether the neural network is acceptable. Training attempt 8 - all observed features
Step 3.8 Creating a Training Set
In this training attempt we will create three different data sets from the initial data set. The first data set will be used for the validation of neural network, the second for training and third for testing the network. The final results of this training attempt are shown in Table 2. Step 5.8 Validate and Train the neural network In this attempt we will use existing network with 6 neurons in one hidden layer. First we need to do a validation of the network by using a smaller set of data so we can check whether such a network architecture is suitable for our problem, and if so, then we can train the network with a larger data set. We will train the network with validation data set that contains 10% of observations. We will set maximum error to be 0.01, learning rate 0.5 and momentum 0.4. Then we click on 'Train' and training starts. Process ends after 183 iterations. 
Based on validation, we can conclude that this type of neural network architecture is appropriate, but it is also necessary to train the network with a larger set of data so we can be sure. We will again train this network, but this time with training set that contains 70% of instances. Learning parameters will remain the same as they were during the validation. 
After 884 iterations, it is shown that this network solves classification problem with max error under 0.01 
Step 6.8 Test the neural network
Finally, we will test the neural network with testing data set that contains 30% of instances that weren't used during the training and validation. As a result of testing the network, we get a total error of 0.16456622671471574. This is not better result than what we got in the previous attempt on same network with no validation. Now if we look at the individual errors, we can see that they are mostly very small which is great. 
Training attempt 9 - tempo, root mean square (RMS) amplitude, dynamic range and number of digital errors
Step 3.9 Creating a training set
In this training attempt we will also show the use of advanced training techniques. Three training sets will be created - validation, training, and testing set, same as upper distribution. The final results of this training attempt are shown in Table 2. Step 4.9 Creating a neural network
We will create a neural network with one hidden layer, which will have 20 neurons. All other parameters will be like in the previous attempts. 
Step 5.9 Validate and Train the neural network
First we need to do a validation of the network by using a smaller set of data so we can check whether such a network architecture is suitable for our problem, and if so, then we can train the network with a larger data set. We will train neural network with validation data set that contains 10% of instances. The maximum error will be 0.01, learning rate 0.2 and momentum 0.7. Training process ends after 202 iterations. 
Then we need to train the neural network with training set that contains 70% of instances using the same learning parameters. After 336216 iterations process ends, and we can see that training was successful. 
Step 6.9 Test the neural network
Now we need to test this neural network in order to see results. The total mean square error is 0.05987942577594153. So, we can conclude that although with this data set we have same situation, the non validated training set gives us better results, but network already seen those data for testing. In fact, this results for 30% of full data set are very satisfactory 
Training attempt 10 - tempo, root mean square (RMS) amplitude, tonality, dynamic range and number of digital errors
Step 3.10 Creating a training set
Data set is subdivided into "training", "validation", and "test" sets. The proportions of instances amount is 70%, 10% and 30% respectively. Step 4.10 Creating a neural network
In this training attempt we will create new neural network with 5 input neurons and 10 neurons in hidden layer, as corresponding network in standard tehniqeus. 
Step 5.10 Validate and Train the neural network
Validation of training was successful after 510 iterations with learning parameters - 0.001 for max error, 0.2 for learning rate and 0.7 for momentum, same parameters will be used in training process with largest training set. 

Finally after 2000 iterations training process ends. 
Step 6.10 Test the neural network
The total mean square error is 0.13505254113621823. With unseen data network predict very fine. 
Training attempt 11 - tempo, root mean square (RMS) amplitude, tonality, dynamic range and number of digital errors
Step 5.11 Validate and Train the neural network
Now we use the same architecture and validation-training-testing sets as in previous attempt, also learning parameters are the same except max error which is 0.01. Validation process is complite after 190 iterations. 

3158 iterations was necessary for training process to end. 
Step 6.11 Test the neural network
The total mean square error is 0.16268651673232665. this means that achieved result is worst then in previous attempt. 
Training attempt 12 - tempo, root mean square (RMS) amplitude, tonality, dynamic range and number of digital errors
Step 4.12 Creating a neural network
The purpose of this final attempt is to compare results, on the same network architecture with same learning parameters, which have been made using different data sets, in terms of inclusion tonality feature of songs. 
Step 5.12 Validate and Train the neural network
Validation of training was successful after 200 iterations with learning parameters - 0.01 for max error, 0.2 for learning rate and 0.7 for momentum, same parameters will be used in training process with largest training set. 

Finally after 1299 iterations training process ends. 
Step 6.12 Test the neural network
The total mean square error is 0.144656, this means that tonality not crucial for classification. 
Conclusion
During this experiment, we have created several different architectures of neural networks. We wanted to find out what is the most important thing to do during the neural network training in order to get the best results. What proved out to be crucial to the success of the training, is the selection of an appropriate number of hidden neurons during the creating of a new neural network. One hidden layer is in most cases proved to be sufficient for the training success, number of hidden neurons which is optimal is between 6 and 10. Although the premise of this experiment was that only a few parameters as rms, tempo, number of digital errors and dynamic range are crucial for music classificationby genre, we found that the best results are achieved when we used full data set with all observed features, but in the latest attempts we have seen that tonality isn't so fundamental in classification process, when we utilize validation. But it has more influence on pattern recognition when we use full dataset with all observed features. Final results of our experiment are given in the tables below. In the first table (Table 1.) are the results obtained using standard training techniques, and in the second table (Table 2.) the results obtained by using advanced training techniques. The best solution is indicated by a green background. Table 1. Standard training techniques 
Table 2. Advanced training techniques 
As it is well known, neural networks great for solving problems of classification, but there is a large problem about interpretation of received results. Future work should be based on neuro fuzzy neural network, where interpretation of results is given through fuzzy sets and rules. Download
See also:
Multi Layer Perceptron Tutorial
|






